OSI Superboard II and the UK101
Telstar, Videotex and Communications
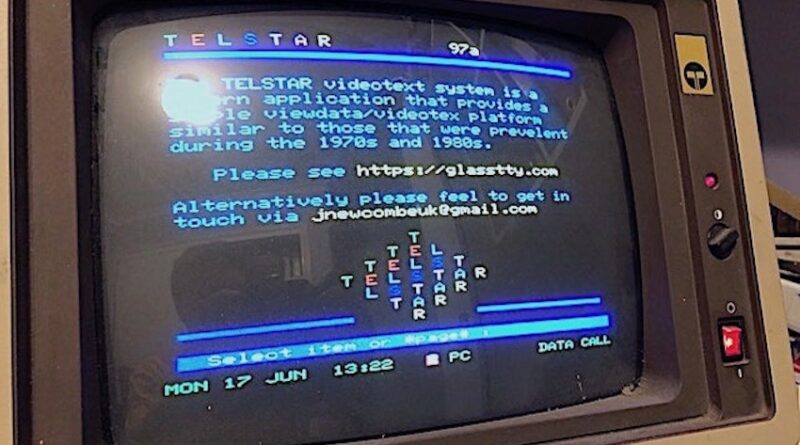
The TELSTAR Viewdata System
The TELSTAR videotex system provides a viewdata/videotext platform similar to those that were prevalent during the 1980s such as Prestel.
The aim of the system is to provide a Viewdata experience for anyone who is interested in how things ‘used to be’. Services in the past typically provided access via the public switched telephone network (PSTN) connection and this is indeed how Telstar works, however, Telstar also makes use of a simple internet connection for modern internet modems.
Gemini 80-Bus

Gemini 80-Bus Resource
A dedicated page to bring my Gemini software, firmware, documentation and associated artifacts into a single resource.
Nascom

The Nascom Experience
An entertaining look at what it’s like to be owned by a Nascom computer. With special thanks to members of the Nascom User Group.
Altair, Apple II, BBC Microcomputer and all things CP/M

Experiencing the Altair 8800
For anyone with an interest in early 8 bit computers, even for those of us in the UK, it is impossible not to recognise the importance of the Altair 8800. In this article I attempt to share my experiences with this awesome machine.
Arduino/Raspberry Pi

Removing the Bounce from a Rotary Encoder in C++
This code was developed from an idea by Oleg Mazurov and is presented here as a complete class that can be added as a tab in an Arduino sketch.